Flow Fields
BY HEEEY
Flow fields, one of the most commonly used algorithmic patterns in generative art today, are used to generate fluid visual patterns. Flow field generation is made possible by an underlying grid of vectors that specify the direction that elements should be drawn on a canvas.
This is the structural backbone of QQL, and the base from which all shapes and compositions emerge. But like QQL’s color palettes, its flow fields aren’t static; they are complex, layered systems that evolve within each seed, with several transforming elements that can affect the final visual outcome.
Let’s dive in and break down how flow fields are used in QQL, and discover how they enable a vast range of visual diversity.
Grid

All QQL seeds have a base vector grid of size 560 x 700. Each vector in the grid has a predetermined regular position that is independent from the canvas resolution. This grid is 40% wider and 40% taller than the canvas, so it extends off the canvas on each side by 20%.
This allows for the flow field center to exist outside of the canvas, generating seeds, for instance, that seem to rotate from a corner of the canvas. It also ensures that elements like ring lines can flow continuously, even if they start beyond the canvas edge, or temporarily flow off the edge of the canvas.
Vector Direction
The user-selectable direction trait determines how vectors in the grid initially oriented. For Linear directions, all vectors point in the same direction, forming lines of rings that either move from left to right, top to bottom, or, when slanted, from any edge to another.
With Radial direction seeds there are more variables that may affect individual vector direction, and may cause each one to have a different angle. One of them is the flow field center, a crucial element that determines the overall composition of Radial QQL seeds.

This center can either be positioned at one of 81 fixed coordinates (9 potential x-positions, and 9 potential y-positions, spaced in thirds across the canvas, and extending beyond its edges) or, alternatively, it can be placed at a random location within the canvas bounds. The more central a fixed coordinate is, the higher the probability that it is chosen as the seed’s flow field center.
Around 74% of all Radial QQLs use a fixed coordinate, resulting in multiple seeds sharing the same focal point. About 21% of seeds use a fixed coordinate on one axis and a random coordinate on the other axis. And 5% of seeds have a center that is fully random (at least, within the bounds of the canvas).


The flow field vectors are initially arranged in a straight line away from this flow field center. Depending on which Radial direction is selected, a rotation of up to 90 degrees will be applied to each vector. Rotating by 0 degrees is “explosive”, with all vectors pointing towards the flow field center. Rotating by 90 degrees is the maximum circular rotation, with flow field vectors being completely perpendicular to the center.
Rotation direction, clockwise or counterclockwise, is determined randomly for each seed. The direction flow lines can be constructed towards the focal point or away from the focal point by applying a 180 degree rotation to the vector’s direction.
A linear angle is assigned too in case the ignore flow field trait is assigned to a seed’s group.
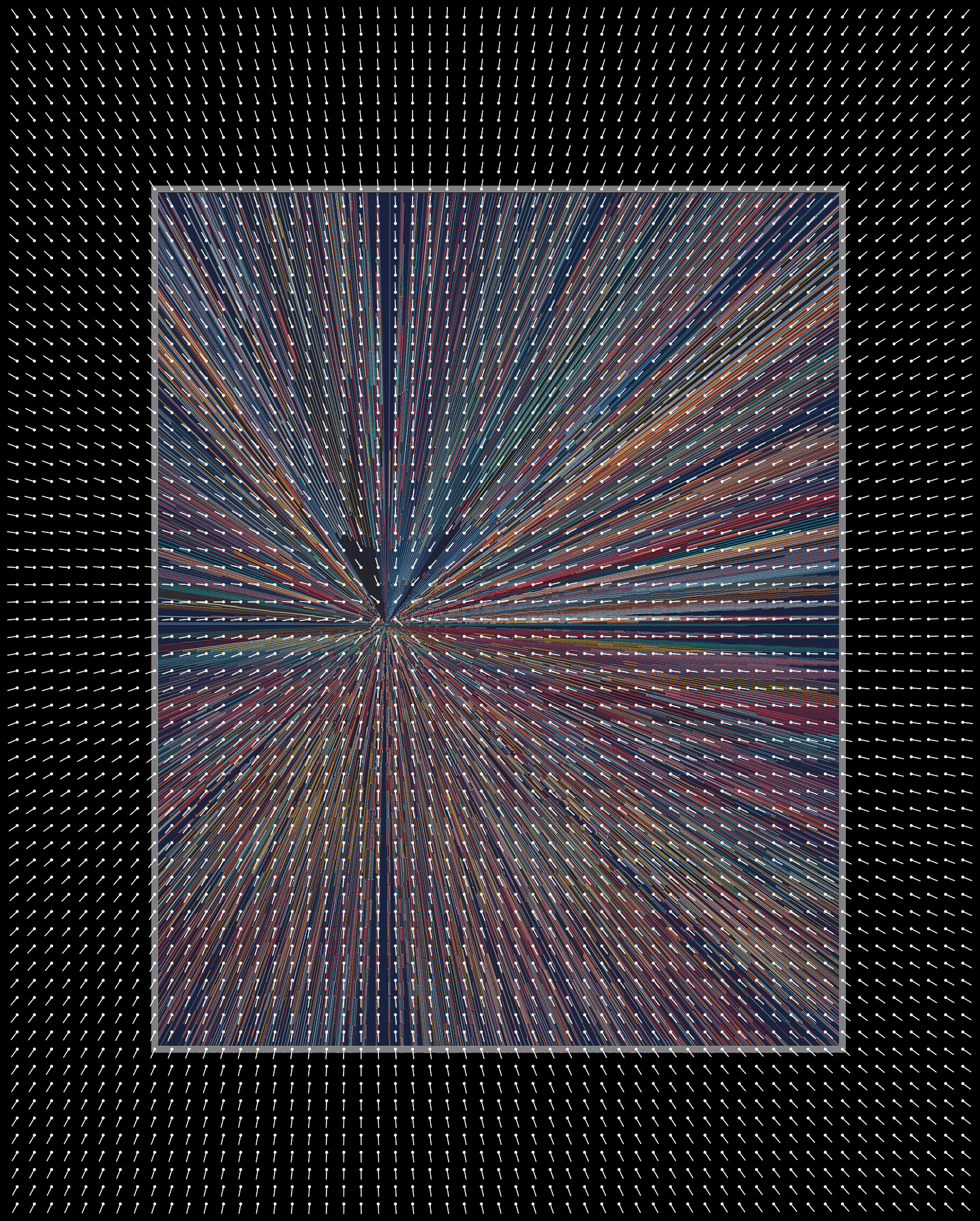
Flow fields start out being “perfect” and, in many seeds that lack turbulence, we can easily see the underlying structure that rings follow. When turbulence is set to Low or High, some vectors’ direction will be changed slightly, creating noticeable effects across the canvas.
In QQL, flow field turbulence is implemented through a series of one or more “disturbances”. Each disturbance rotates the vectors in its local area. The closer a vector is to the center of the disturbance, the stronger the effect will be. Disturbances can also be small or large. The average disturbance radius is around 35% of the canvas width, but it can also be as small as 10% of the canvas width, or larger than the whole canvas.
In seeds with small, dense rings, turbulence will be especially visible. Any slight rotation of the line placement results in the displacement of rings, and a visible ripple effect occurs. However, the more common effect of turbulences is a subtle distortion of the vectors’ direction, resulting in flow field lines that roughly keep their “intended” shape.
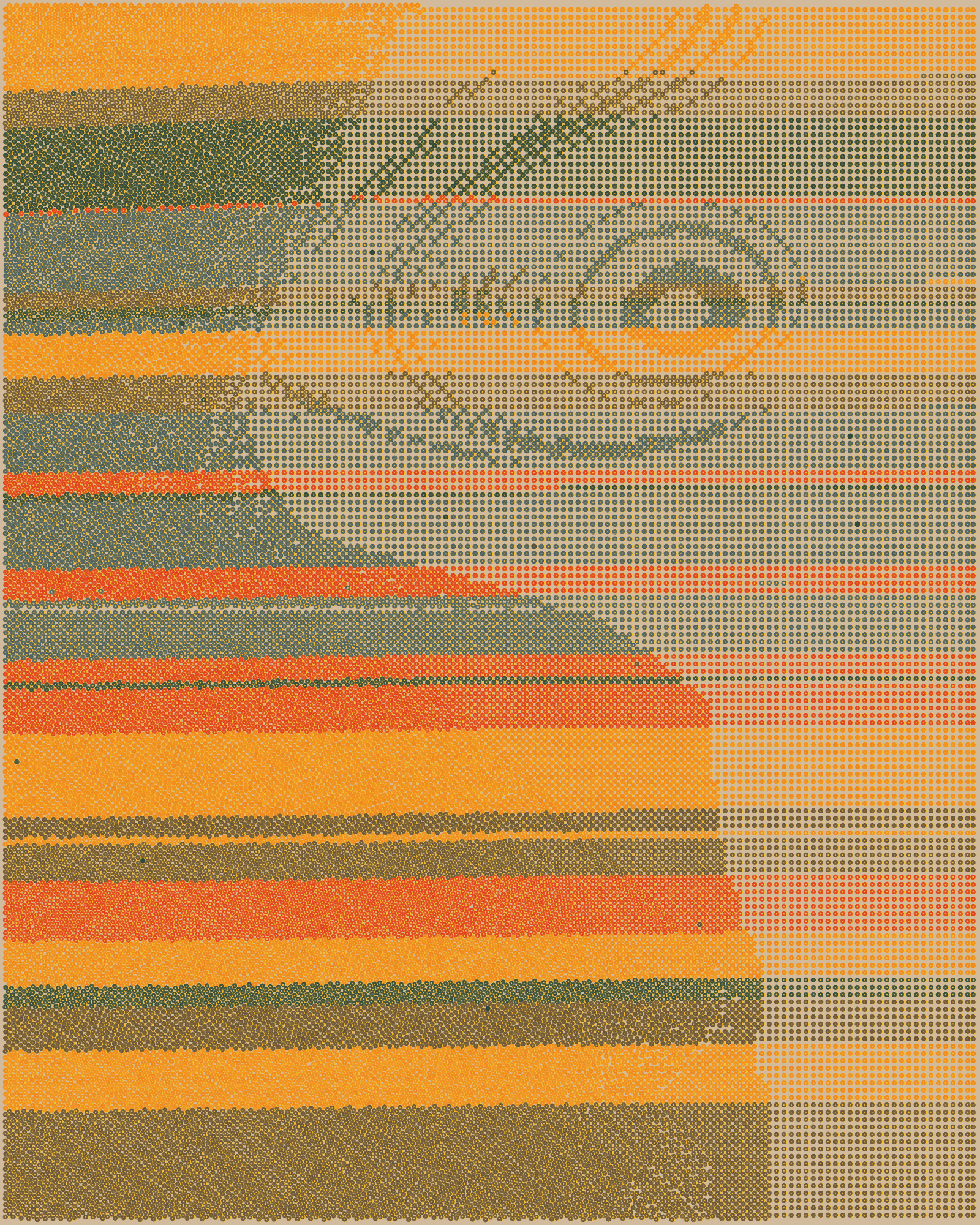


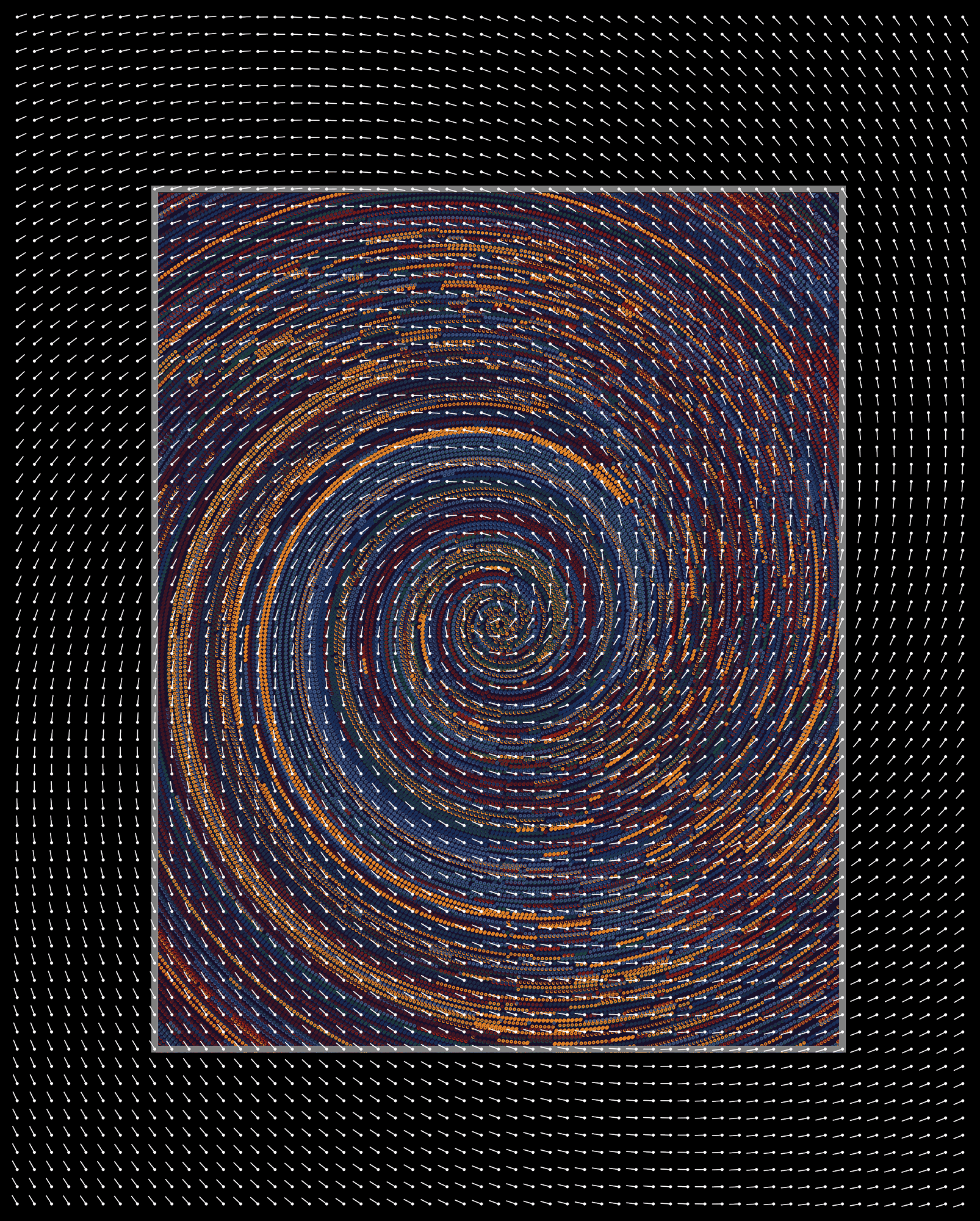
Grouped Flow Lines
Each different QQL structure generates groups of rings in unique ways. The structures achieve this by creating different sets of starting points within each group. From each starting point, a flow line can potentially emerge.
- Formation generates rectangular grids of evenly spaced points.
- Orbital places points in arcs or circles with increasing radii, where all points in the same arc belong to a group.
- Shadows groups start as non-overlapping circles full of points, and these circles may be scattered around the canvas.


From each of these starting points, a flow line is generated by taking many tiny steps. At each step, the local vectors in the flow field are consulted, determining the exact direction of the step. The result is a fluid and continuous path. The flow lines may be built from 500, 650 or 850 steps, and this length is chosen randomly. As long as the flow line hasn’t reached the flow field center (if Radial) or is within the boundaries of the flow field vector map, it will keep adding points up to a predetermined distance. In essence, flow lines are the element that connect the structure groups with the underlying flow field.
Rings
Each group has an assigned “drawing” order, and each line within a group has an order as well. The algorithm places rings by following a strict order, starting from the first point in the first line in the first group.
The first point—which can technically be the furthest one away from the group’s start point if the flow field points outwards—is assigned a ring. Then, the algorithm tries to position a ring in the next point. If the new potential ring would collide with the previous ring, it is discarded and the algorithm moves on to the next point, repeating this until it succeeds. This process is repeated until the flow line has been converted into a set of corresponding rings. Once a line is complete, the next line in the group is processed in the same way. When all lines in a group have been processed, the algorithm moves on to the next group.


This group-line iteration is what makes QQL composition so varied and interesting. The first groups of lines in a seed will take preference occupying areas where other groups of lines would “want” to draw rings as well, but because these flow lines of rings follow a predetermined path, there is “always” available space for latter groups of rings to blossom.
This sequencing also makes it possible for rings from different groups (and thus different properties, like size, color, and band quantity) to coexist and blend together.


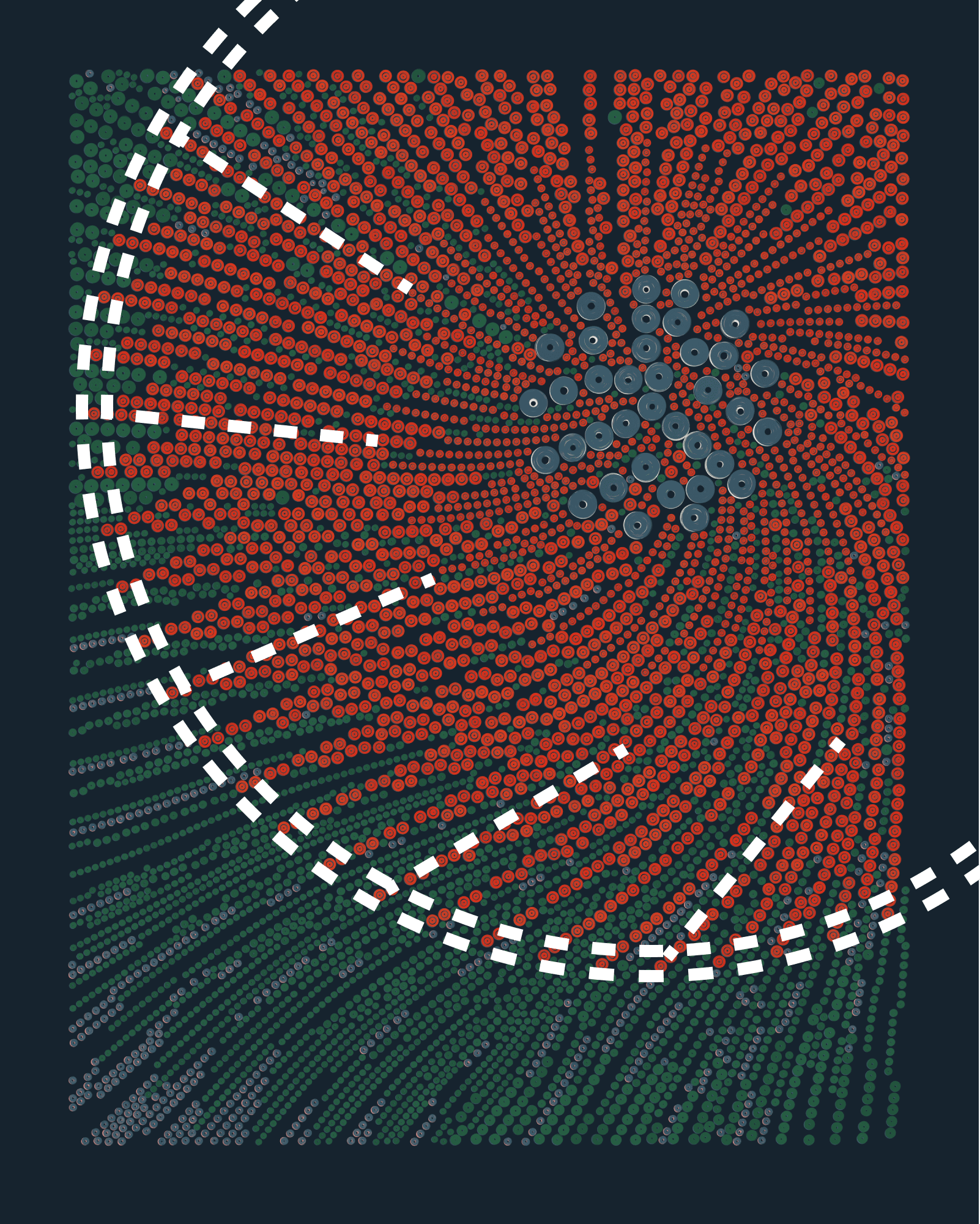
Flow Lines Color
For each different structure, the starting points (and thus flow lines) in each group have their own potential order. This order not only influences which rings are finally drawn, but also how color is laid out.
- Formation: order is row-based, starting from the top row and moving down.
- Orbital: order is organized around concentric circular groups, with start points beginning on the right side of the circles, and inner circles’ groups being determined before the outer circles’ ones.
- Shadows: there are two potential ways of arranging start points; _circular or square. If circular, start points and their flow lines will be ordered inside-out. If square, the order will work in the same way as in Formation, dropping any points that might fall outside of the circular base.
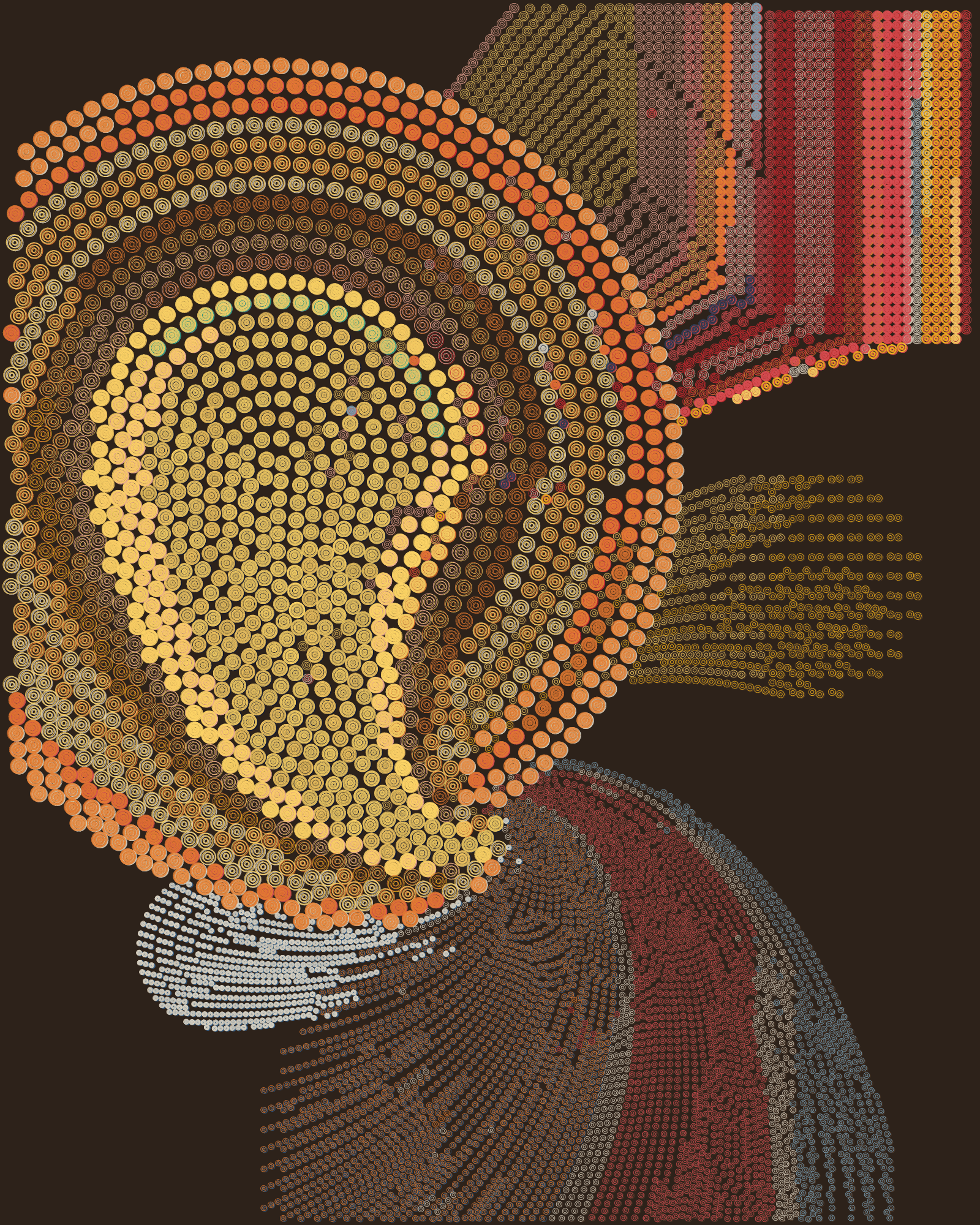
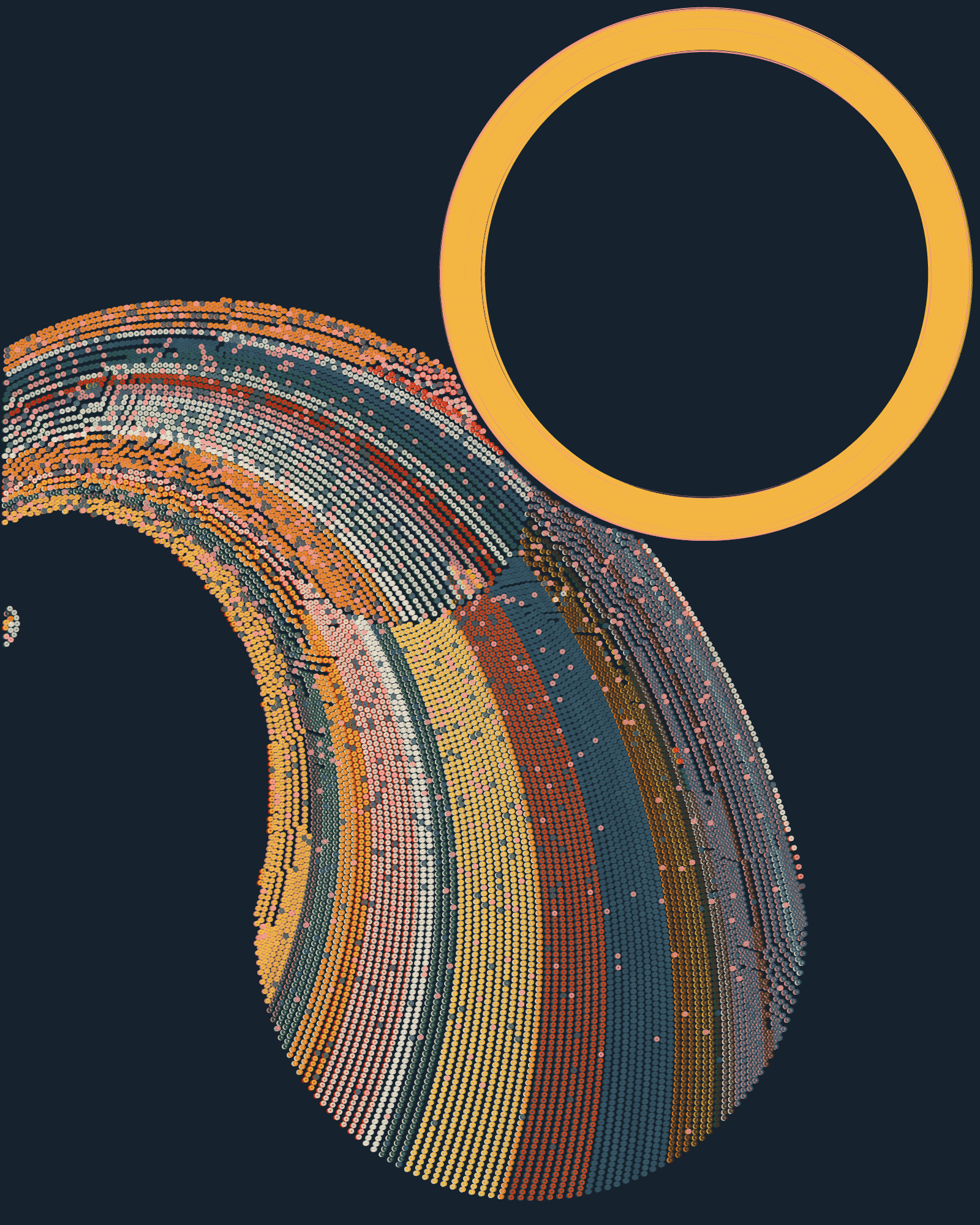
Color Variety influences how the initial color is chosen for each group, and the quantity of colors available to draw from. Each flow line has an assigned ring color which it will keep throughout all rings, except when splatter is present. When a line has been completed, there is a variable chance (depending on Color Variety, Spacing and Ring Size) for the next line’s ring color to be swapped with a new one from the list of available colors.
For instance, If a seed has Dense, Small rings, Low Color Variety and Shadows Structure there is less than 0.1% chance of ring color changing form line to line. On the opposite side of the spectrum, if a seed has Large, Sparse rings and High Color Variety there is an 11% chance of that the ring color will change across lines. This means that QQL can both produce outputs that have large regions with the same color, as well as outputs that frequently shift color.

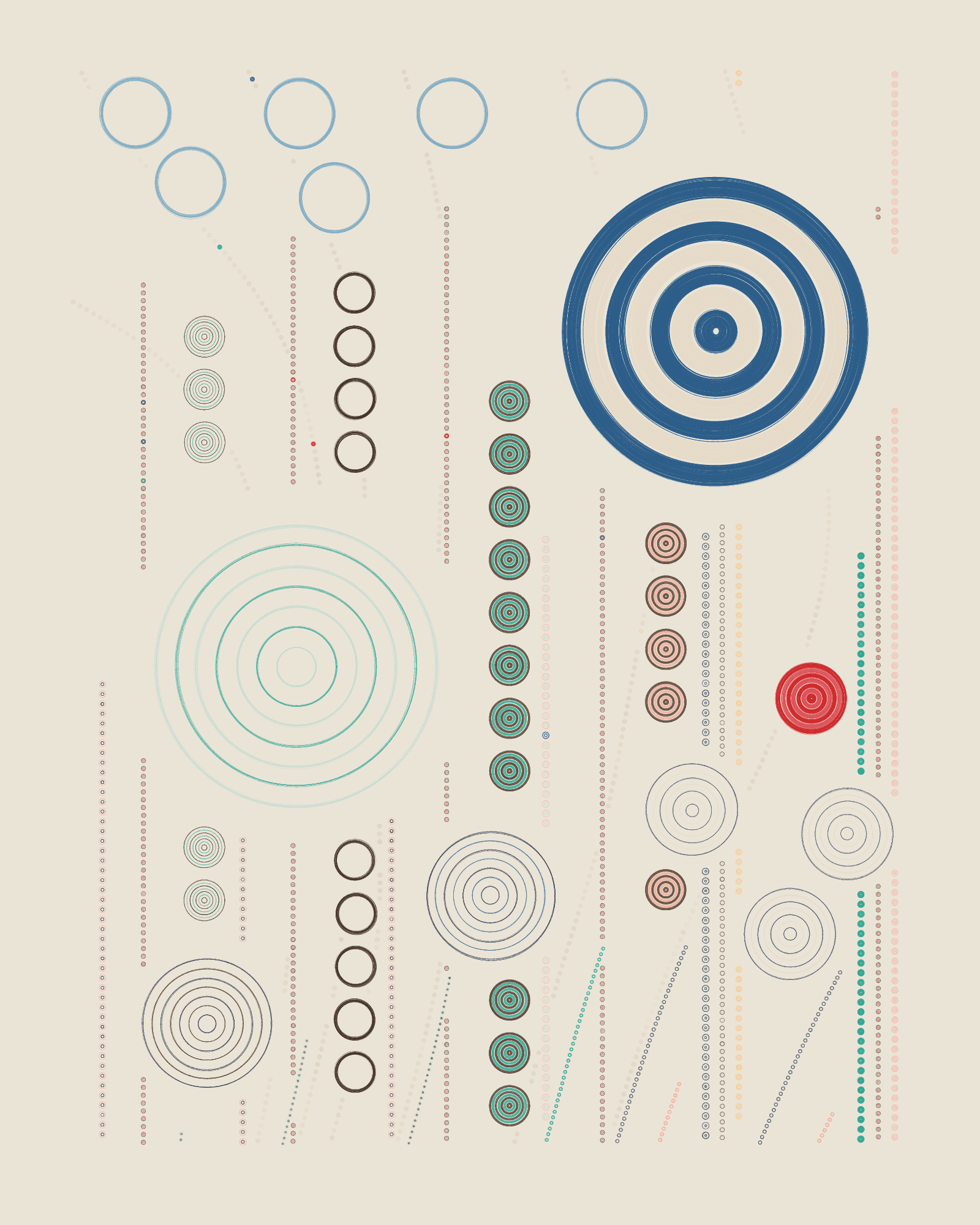
When a new line is selected for a color change, color selection will tend to pick the previous or the next color from the sequence of available colors. Occasionally, a color that is farther away in the sequence may be selected, too. The color-picking method used in QQL seeds is not random, but rather colors are selected with a certain logic, where the artists studied and matched colors not only for color palettes, but also for color distribution in seed composition.
Because color sequence order stays constant across color palettes, Color Variety can cause the list to contain fewer or more colors, but they will always be in the same order. Due to this, the succession of colors between neighboring flow lines often have detectable patterns that can re-occur in multiple seeds with the same palette. This consistent color matching results in relatable aesthetics across QQL seeds.
We may find color progressions that go back and forth with the same colors, or that seem to follow a certain color rhythm, only for this to be “broken” with a different color in a particular area of the canvas. We can also find large single-color regions followed by constant color changes.


As we have discovered, QQL flow fields have multiple “moving” parts that are essential in the construction of incredibly diverse outputs. The combination of direction, turbulence and structure lay the ground for seed composition with groups being the “invisible” structuring element of QQL. When we combine all these traits with ring-based properties, we can understand all the complexity and richness that are present in the QQL algorithm.
Although it can be hard to distinguish between flow lines and groups just by looking at most seeds, in others we can intuitively understand how their flow fields work, how same-group lines of rings are connected to each other, and where one group ends and the next one begins.